An Introduction to the FHI-aims Code
(Navigate with your arrows keys or swipe through)

Who we are
Amazing Community of Contributors
- Beginning of the Code: Volker Blum, Karsten Reuter, Matthias Scheffler at Fritz Haber Institute, 2004
- Since then: Hundreds of individuals, without whom FHI-aims would not exist
- Direct contributors to FHI-aims: ~150

How we are organized
- FHI-aims is licensed through MS1P e.V. - a registered nonprofit supporting basic science
- User registration and code download at fhi-aims.org
- Primary communication platform: Slack Workspace
- Code developement at the FHI-aims GitLab including stable versions, issue tracker, wiki, and build instructions

Why FHI-aims?
Vision:
Quantum mechanics based simulations of molecules, materials and their properties without a priori precision and accuracy limitations

Why FHI-aims? – Critical choice
Numeric atom-centered basis functions
for an accurate representation of occupied orbitals and densities
Algorithmic choices and priorities
- All-electron, full potential
- Non-periodic and periodic systems on equal footing
- Scalability to large systems (thousands of atoms) without precision limitations
- Seamless scalability from laptop to massively parallel HPC architectures
- Density functional theory and correlated methods (RPA, GW, ...)
↓
Numeric Atom-Centered Basis Functions
\[\begin{aligned} \varphi_{i[lm]} (r) & = \frac{u_i(r)}{r} Y_{lm} (\Omega) \end{aligned} \]$u_i(r)$: Localized radial function. Flexible choice - “Anything you like.”
Solution to the free atom radial Schrödinger equation:
\[\begin{aligned} \left[ - \frac{1}{2} \frac{\text{d}^2}{\text{d}r^2} + \frac{l(l+1)}{r^2} + v_i(r) +v_\text{cut}(r) \right] u_i(r) = \epsilon_i u_i(r) \end{aligned} \]- free-atom like: $v_i(r) = v^\text{DFT}_\text{free atom}(r)$
- hydrogen-like: $v_i(r) = \frac{Z_i}{r}$
- free ions, harmonic oscillators (Gaussians), ...
↓
Our basis set library
- List of NAO basis functions for all elements (1-102)
- From fast qualitative to meV-converged total energies (for LDA/GGA/hybrid density functionals)
How to construct them? All details in the paper
V. Blum, R. Gehrke, F. Hanke, P. Havu,V. Havu, X. Ren, K. Reuter and M. Scheffler, “Ab Initio Molecular Simulations with Numeric Atom-Centered Orbitals”, Computer Physics Communications 180, 2175-2196 (2009)
Making use of NAOs:
Scalable Hybrid Density Functionals
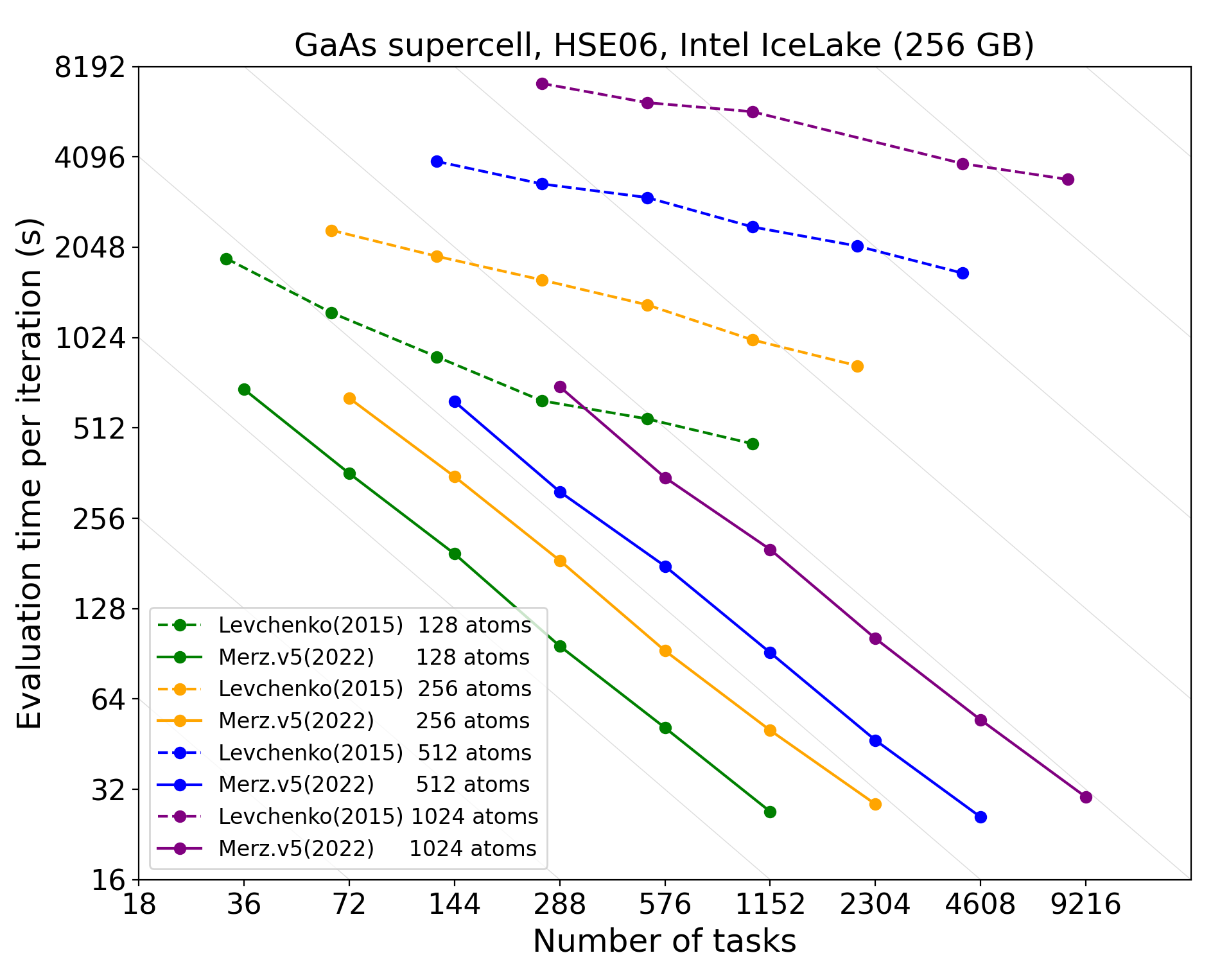
- O(N) scaling implementation Levchenko et al., Comp. Phys. Commun. 192, (2015).
- Localized resolution of identity Ihrig et al., New J. Phys. 17.9, (2015)
- Memory efficient: MPI-3 intra-node shared memory
Broad ecosystem
of connected infrastructure
Modular software architecture

GIMS
Open, Free, Browser-Based Graphical Interface
Try it right now!
gims.ms1p.org
Where to start
A set of open introductory, open-access tutorials
Start with: Basics of Running FHI-aims